ANGULOS
Deficinicion 1
Se denomina ángulo en el plano a la porción de plano comprendida entre dos semirrectas con un origen común denominado vértice. Otra concepción de ángulo dice que éste es la figura formada por dos rayos con origen común. Con cualquiera de estos dos conceptos, un ángulo determina una superficie abierta (subconjunto abierto de puntos del plano), al estar definido por dos semirrectas, la medida de ángulos es la medida de la abertura de estas semirrectas, que se denomina medida del ángulo.
Definicion 2
Unión de 2 rayas que tienen el mismo punto extermo las rayas se llaman llados del angulo y su punto externo común recibe el nombre de vértice del angulo
Ángulo agudo
RELACIONES ENTRE ANGULOS
Angulos complementarios
Dos angulos son complementarios si suman 90
A⁺B= 90
Ángulos complementarios: todo ángulos que sumados dan 90 grados
Ángulo agudo
Es el ángulo formado por una abertura mayor de 0º y menor de 90º.
Ángulo recto
Un ángulo recto es igual a 90º, o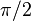 
Rad.).
Los dos lados de un ángulo recto son perpendiculares entre sí, la proyección ortogonal de uno sobre otro es un punto, que coincide con su punto de intersección.
Ángulo obtuso
Un ángulo obtuso es superior a 90º e inferior a 180º, esto es entre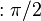 
y 
Rad.).
Ángulo llano
Un ángulo llano o plano es igual a 180º, o Rad.).
Un ángulo de 180º.
En un ángulo llano los dos lados están alineados uno a continuación de otro dividiendo el plano en dos semiplanos.
Ángulo Cóncavo
Es el ángulo que mide más de 180º y menos de 360°
Ángulo perigonal o completo
Un ángulo perigonal es igual a 360º, esto es 
Rad.).
Este ángulo se obtiene al hacer girar la semirrecta hasta colocarla en su posición inicial.
•Bisectriz: es una semi-recta que pasa por el vértice de un Angulo
•
Ángulos opuestos por el vértice
•Ángulos internos: son los que quedan comprendidos entre la banda de espacio entre la recta (R1) y la recta (R2)
Ángulos externos: son aquellos que quedan fuera de la banda formado por la recta
•
Ángulos alternos: son los ángulos ubicados en distintos semiplanos con respecto a la recta secante (R3), pueden ser externos e internos por ejemplo
•
Alternos externos (a, d), (c, b)
•
Alternos internos: (d, a), (b, c)
•
Ángulos correspondientes: son los ángulos que están en el mismo semiplano (a, e) (c, g)
